User Case Study:
Maple Optimized Teaching Motivates Students and Simplifies Learning


Challenge
Jalal Soussi, a high school teacher and member of a “Digital Transition” task force in Belgium, wanted a solution that would optimize education, allowing instructors and students to maximize time and resources.
Solution
Soussi researched Maple’s capabilities to assess Maple’s ability to engage students and simplify the learning process. He developed a math application to illustrate Maple’s capabilities by solving various problems.
Result
Soussi found that Maple is an ideal environment for creating customized educational pathways for students, as it is user-friendly and easy for students to explore to deepen their understanding of key concepts.
Modern digital learning tools are transforming how education is delivered, offering new ways to make education more efficient and beneficial to students, and providing instructors with the ability to maximize time and resources. Jalal Soussi, a high school teacher in Belgium, researched Maple’s capabilities for optimizing education and recently presented his findings.
In addition to his role as a high school teacher, Soussi also serves as a trainer in the field of Computer-Assisted Language Learning (CALL), and is a member of a “Digital Transition” task force as part of Belgium’s Pact for Excellence in Education. Soussi has worked extensively with Maple and recently examined usage of the software for “Optimization Teaching”, based on a series of math applications he developed. Soussi’s research assessed Maple’s ability to motivate students and simplify learning, thus changing the optimization of learning. According to Soussi, various aspects of Maplesoft technology help to accomplish this, including:
Soussi selected Maple because it is a comprehensive mathematical software tool with formal computation capacities allowing for accurate solutions to many problems. Additionally, Maple is also a powerful tool for numerical computation with advanced features, including 2-D and 3-D interactive interfaces for graphic visualization, audio and video, he said. “Its packages, MathApps and Tutorials allow it to address, illustrate, make assumptions, demonstrate and understand several mathematical concepts.”
Soussi states that Maple embodies all the qualities required to experiment with mathematics (i.e. to address this subject area in an original, stimulating way that is suitable for discoveries and intuitions). “Maple is easy to learn, and online help, such as permanently-available tutorials, almost exempts you from reading the user guide,” he said.
The following is an example of a math application Soussi developed that illustrates Maple’s capabilities.
Problem
To examine a training sequence for optimization in Maple, Soussi selected 20 varied problems, using the following problem as a guideline: “Find the dimensions of the right circular cylinder of the largest volume that can be inscribed in a sphere of radius 4”.
Soussi selected the proposed structure due to its flexibility, allowing him to explore the various Maple environments. In preparation, he worked around the basic geometric properties of the cylinder (Figure 1), based on voice guidance, to obtain different formulas (volume, surface, etc.)
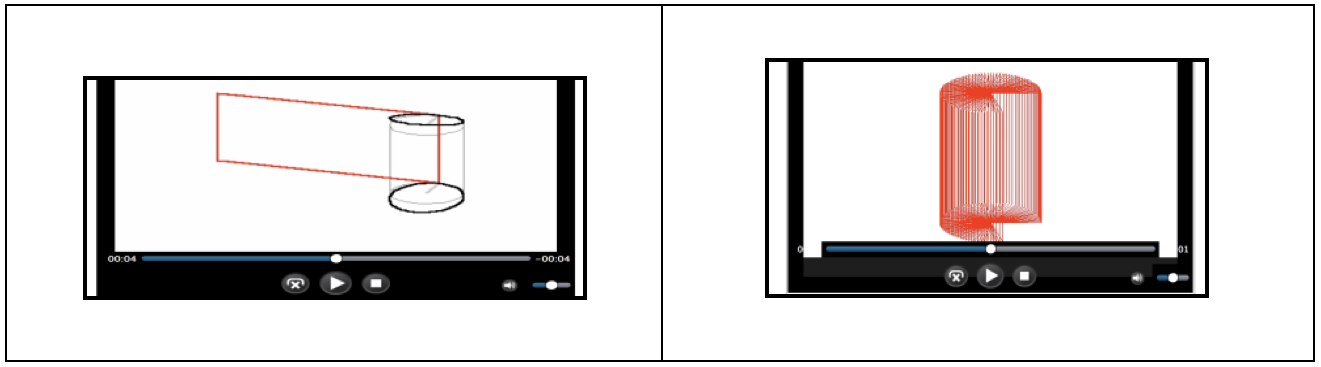
Figure 1
He worked interactively around the concept of a solid revolution, generated by the rotation of the constant function around the axis. This provided an opportunity for him to address the concept of integral calculus face-to-face, without in-depth consideration (Figure 2).
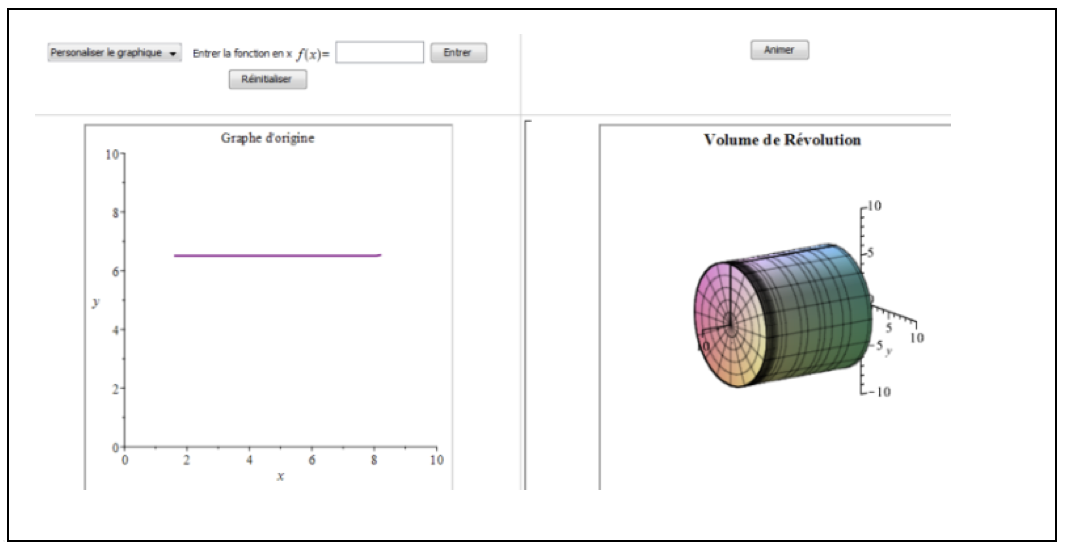
Figure 2
Soussi then refers users to another application linking both figures of the problem. By interactively approaching the volume of a sphere by cylinders, users can conveniently and efficiently address concepts such as limits and series convergence.
Problem Solving
In order to solve the problem, there are several different approaches users can employ. The following are techniques suggested by Soussi in his research.
Dynamic Animation
Users can create several 3-D moving figures, which are controlled by the different variables of the problem (cylinder height and radius, in the case of the example problem) (Figure 3). This can improve the spatial perception of these representations.

Figure 3
Trial and Error
Soussi presents the possibility of associating the dynamic figures with a value table (Figure 4). He found that by interactively controlling the variables of the problem, the learner is capable of digitally approaching the optimal solution.
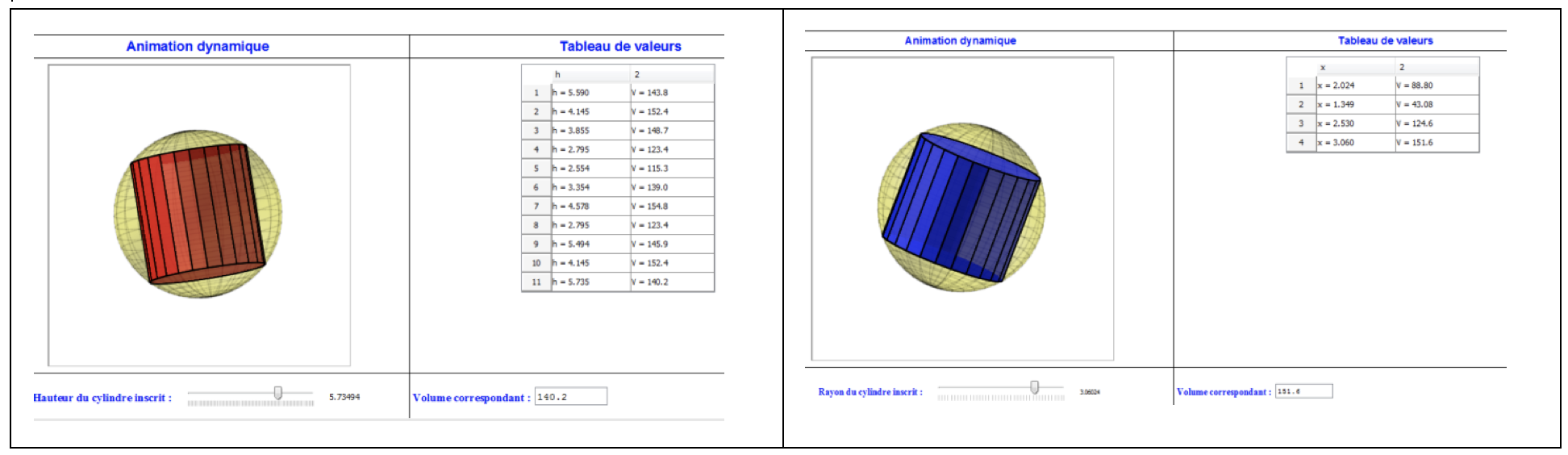
Figure 4
Analytical Development
Soussi states that thorough analysis of the optimization function(s) - field of definition, derivatives, monotony, remarkable points, curve - is carried out regardless of the form of the function, either by calling the Maple commands - for learners who are familiar with the software - or through the intuitive process of Clickable Math, a concept unique to Maple that simplifies the process for learners who are not as familiar with it. The ‘Tutorials’ tool enables you to autonomously check the various results (Figures 5-A and 5-B).

Figure 5-A
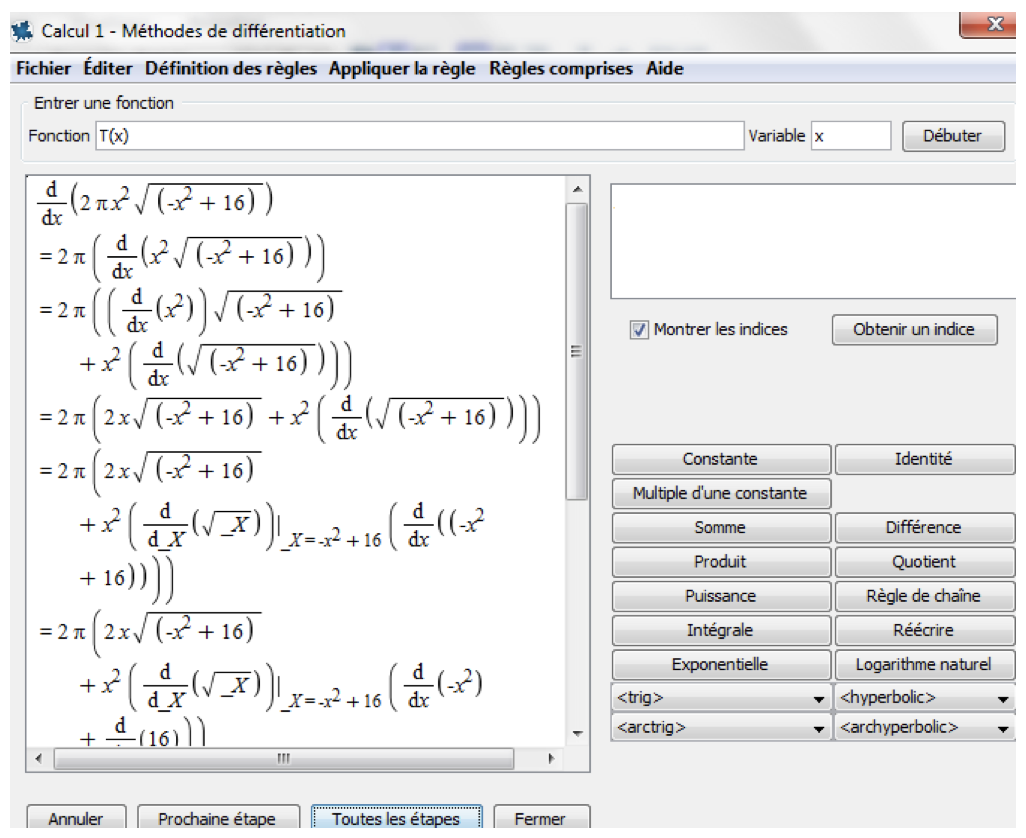
Figure 5-B
As an example, Soussi provides the following optimization function, which results from choosing to act on the cylinder radius:
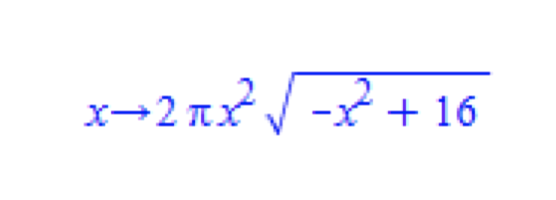
He provides the following examples of crossed passages:
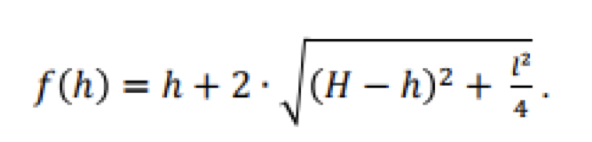

Several alternative approaches that are easy to explore with Maple are possible, Soussi said. Squaring the function, then graphically and analytically checking that its maximum takes place at the same point as the maximum of its initial function is a great example of this approach (Figures 6-A and 6-B).

Figure 6-A
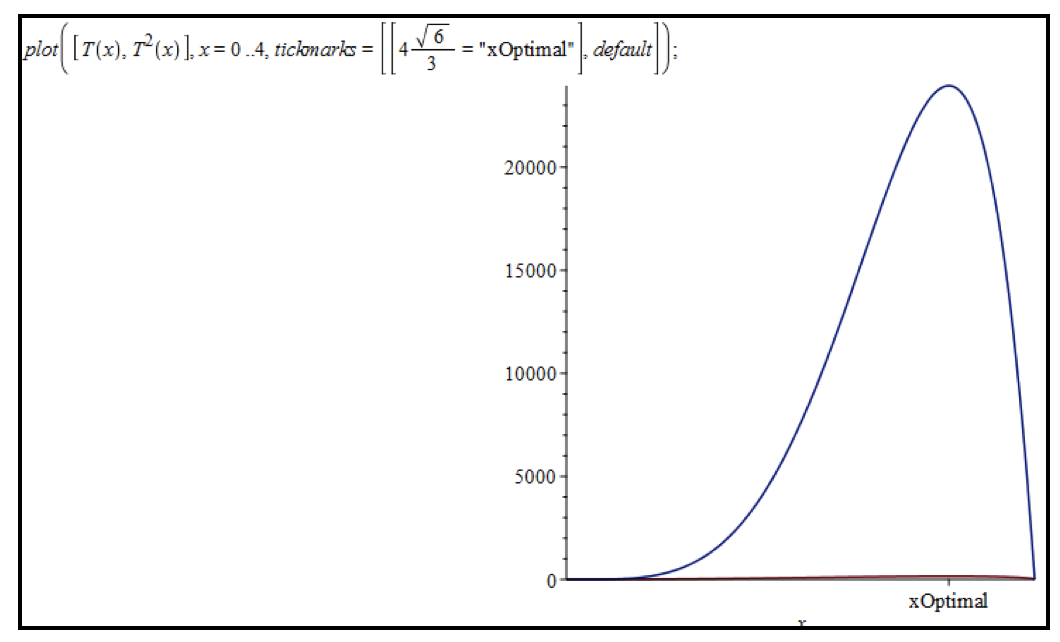
Figure 6-B
Visual Synthesis
The graph of a function is often seen as a static object and its link with a phenomenon is not obviously easy to establish for a learner, Soussi said. “The wide array of Maple interactive components allows users to interactively act on the many variables of the problem to simultaneously illustrate several concepts: the tangent (at function level), the sign (at first derivative level) and the concavity (at second derivative level).” This can be seen in Figure 7 below.
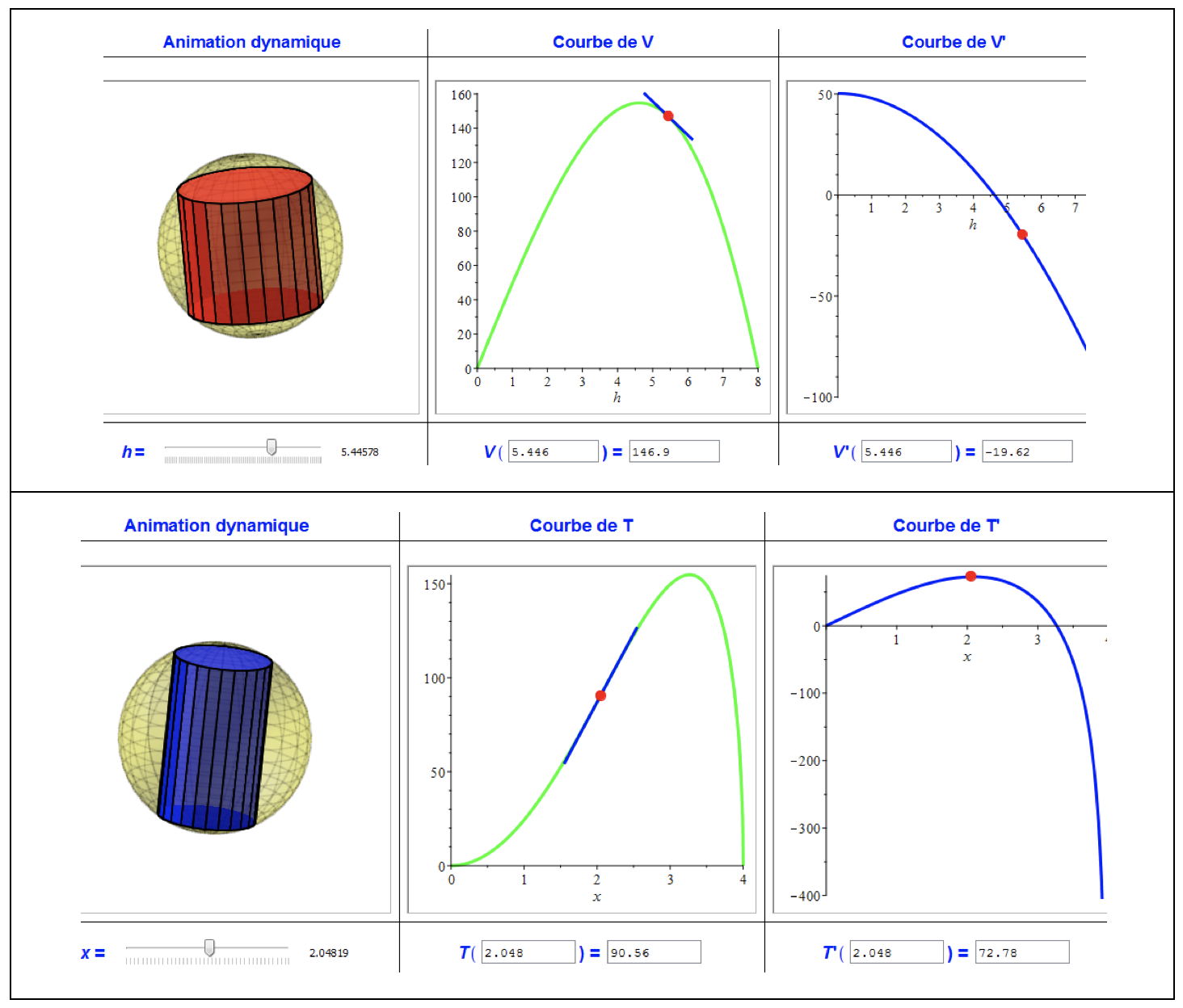
Figure 7
The video Optimisation avec Maple, which was created by Soussi, demonstrates some of the ways he uses Maple.
Conclusion
In order to master this subject area, Soussi said working autonomously on all problems is necessary. Soussi has experimented with other software to approach a problem in the same way and said Maple is an ideal solution. “Indeed, when confronted with similar situations, most textbooks and educational support materials interrupt exploration,” he concludes. “But with Maple, the learner is easily able to explore these concepts deeply and optimize their learning.”
 Contact Maplesoft to learn how Maple can be used in your classroom.
Contact Maplesoft to learn how Maple can be used in your classroom.