Maple 2020 includes a very large number of improvements that strengthen the math engine, expanding Maple's abilities to handle new areas of mathematics and solve harder problems, faster. In addition to the advancements in ODEs/PDEs, graph theory, group theory, integral transforms, and other topics that are detailed elsewhere, there are also enhancements to fundamental routines that are used regularly both by customers and by other Maple commands.
assume, is, coulditbe, getassumptions, about
User friendly improvements to getassumptions
The getassumptions command now returns all assumptions directly or indirectly related to the variables in the input. now returns all assumptions directly or indirectly related to the variables in the input.
| > |  |
In the following, the two assumption not directly involving 
are now also returned because together with the other assumption they provide extra information about 
, namely that 
is real and greater than 0. These facts cannot be inferred from the assumption 
alone.
| > |  |
 |
| > |  |
assume can now handle generic Or-type assumptions
Previously Maple could only handle Or-type assumptions involving the same subexpression, such as:
Now, any conditions that can be assumed independently can also appear in an Or-type assumption:
| > |  |
| > |  |
 |
| > | ![`assuming`([is(`<`(0, x))], [additionally, `<=`(y, 0)]);](advanced-math/AdvancedMath_13.gif){kind=small} |
 |
| > |  |
is now makes calls to the SMTLIB package
The is command now makes use of SMTLIB:-Satisfy to help compute some answers involving real variables.
| > | ![`assuming`([is(x = 0)], [`<`(0, abs(x))]);](advanced-math/AdvancedMath_16.gif){kind=small} |
 |
| > | ![`assuming`([coulditbe(x = 0)], [`<`(0, abs(x))]);](advanced-math/AdvancedMath_18.gif){kind=small} |
 |
| > | ![`assuming`([is(`<=`(0, `+`(`*`(`^`(a, 2)), `*`(`^`(b, 2)), `*`(2, `*`(a, `*`(b))), abs(`*`(`^`(r, 2))))))], [real]);](advanced-math/AdvancedMath_20.gif){kind=small} |
 |
| > | ![`assuming`([is(abs(`*`(x, `*`(y))) = `*`(abs(x), `*`(abs(y))))], [real]);](advanced-math/AdvancedMath_22.gif){kind=small} |
 |
| > | ![`assuming`([is(`<=`(0, `+`(`*`(`^`(`+`(a, `-`(b)), 2)), `*`(`^`(`+`(c, `-`(d)), 2)))))], [real]);](advanced-math/AdvancedMath_24.gif){kind=small} |
 |
Triangle Inequality:
| > | ![`assuming`([is(`<=`(abs(`+`(x, y)), `+`(abs(x), abs(y))))], [real]);](advanced-math/AdvancedMath_26.gif){kind=small} |
 |
Other new results from is and coulditbe
| > | ![`assuming`([is(`/`(`*`(('abs')(`+`(`*`(x1, `*`(y2)), `-`(`*`(x2, `*`(y1)))))), `*`(`+`(`*`(x1, `*`(x2)), `*`(y1, `*`(y2))))), rational)], [x1::'posint', x2::'posint', y1::'posint', y2::'posint']);](advanced-math/AdvancedMath_28.gif){kind=small} |
 |
| > | ![`assuming`([is(abs(`+`(x1, `-`(x2))), posint)], [x1::'posint', x2::'posint', y1::'posint', y2::'posint']);](advanced-math/AdvancedMath_30.gif){kind=small} |
 |
| > |  |
 |
| > |  |
 |
| > |  |
 |
| > | ![`assuming`([is(a, real)], [`/`(1, `*`(`+`(`*`(a, `*`(y)), `-`(sqrt(`+`(`-`(`*`(a, `*`(b))))))))) = z, y = sqrt(x), `<`(0, x)]);](advanced-math/AdvancedMath_38.gif){kind=small} |
 |
| > | ![`assuming`([is(`<`(0, exp(f(x))))], [`<`(0, x)]);](advanced-math/AdvancedMath_40.gif){kind=small} |
 |
| > |  |
 |
| > | ![`assuming`([coulditbe(x, {1, 2})], [x::set]);](advanced-math/AdvancedMath_44.gif){kind=small} |
 |
| > |  |
 |
| > | ![`assuming`([is(randpoly([x, n]), integer)], [x, real, n, prime]);](advanced-math/AdvancedMath_48.gif){kind=small} |
 |
| > | ![`assuming`([is(exp(x), real)], [x::imaginary]);](advanced-math/AdvancedMath_50.gif){kind=small} |
 |
| > | ![`assuming`([is(`+`(`-`(n), `-`(1)), {-1, 0, posint})], [n::'nonposint']);](advanced-math/AdvancedMath_52.gif){kind=small} |
 |
| > | ![`assuming`([coulditbe(`<=`(`+`(`-`(`/`(1, `*`(f(x))))), 0))], [Not(`<`(0, f(x)))]);](advanced-math/AdvancedMath_54.gif){kind=small} |
 |
| > | ![`assuming`([is(x, complex)], [x::(Non(0))]);](advanced-math/AdvancedMath_56.gif){kind=small} |
 |
| > | ![`assuming`([is(abs(`+`(`*`(x1, `*`(y2)), `-`(`*`(x2, `*`(y1))))), integer)], [x1::'posint', x2::'posint', y1::'posint', y2::'posint']);](advanced-math/AdvancedMath_58.gif){kind=small} |
 |
| > |    |
 |
| > | ![`assuming`([coulditbe(m, 0)], [`<`(`+`(`*`(`/`(1, 2), `*`(`^`(n, 2))), `-`(`*`(`/`(1, 2), `*`(n)))), m), n::'integer', Or(`<`(n, 0), `<`(1, n))]);](advanced-math/AdvancedMath_64.gif){kind=small} |
 |
The following result used to be true. It now returns FAIL since is cannot determine if the property is always satisfied.
| > | ![`assuming`([is(sqrt(x), real)], [x::'integer']);](advanced-math/AdvancedMath_66.gif){kind=small} |
 |
about
This result from about is now simpler:
| > | ![`assuming`([about(x)], [x::(RealRange(0, infinity)), (`+`(`-`(x)))::(RealRange(`+`(`-`(infinity)), 0))]);](advanced-math/AdvancedMath_68.gif){kind=small} |
| Originally x, renamed x~: is assumed to be: RealRange(0,infinity) |
Maple can now compute asymptotic expansions for various mathematical functions of type 
with rational parameter values.
| > |  |
 |
| > |  |
 |
| > |  |
 |
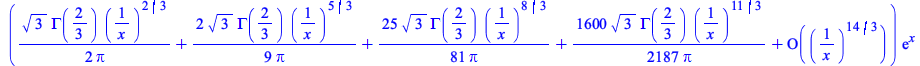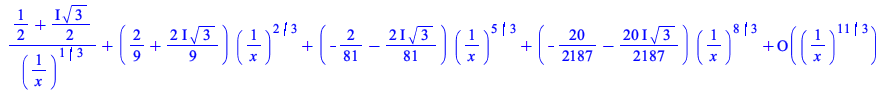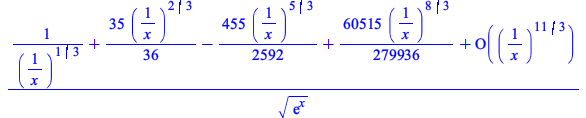ComputationalGeometry:-PointInPolygon
The new command PointInPolygon determines if a point lies within the polygon formed by a list of points.
| > |  |
| > | ![Q := [[1.1180, .36327], [0., 1.1756], [-1.1180, .36327], [-.69098, -.95106], [.69098, -.95106]]; -1](advanced-math/AdvancedMath_77.gif){kind=small} |
| > | ![a := [0., 0.]; -1](advanced-math/AdvancedMath_78.gif){kind=small} ![b := [1., 1.]; -1](advanced-math/AdvancedMath_79.gif){kind=small} ![c := `+`(`*`(.5, `*`(Q[1])), `*`(.5, `*`(Q[2]))); -1](advanced-math/AdvancedMath_80.gif){kind=small} |
| > | ![plots:-display(plottools:-point([a, b, c], symbolsize = 20), plots:-textplot([a[],](advanced-math/AdvancedMath_81.gif){kind=small} ![plots:-display(plottools:-point([a, b, c], symbolsize = 20), plots:-textplot([a[],](advanced-math/AdvancedMath_82.gif){kind=small} |
 |
| > |  |
 |
| > |  |
 |
| > |  |
 |
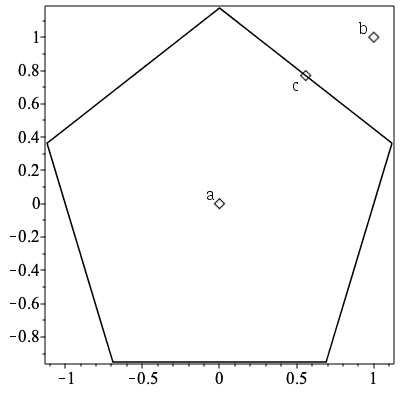The new command evala/Minpoly computes the minimal polynomial of
| > |  |
| > |  |
 |
| > |  |
 |
| > |  |
 |
| > |  |
 |
A subset of this functionality is also available through a new calling sequence in the MinimalPolynomial command in the PolynomialTools package.
| > |  |
 |
| > |  |
 |
Integration
There have been some improvements in integration of algebraic, elementary, and piecewise functions:
| > |   |
     |
| > |  |
      |
| > |  |
    |
| > |  |
   |
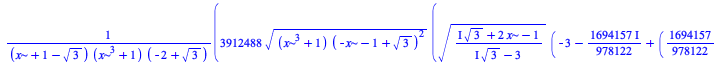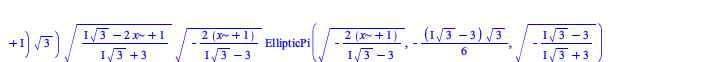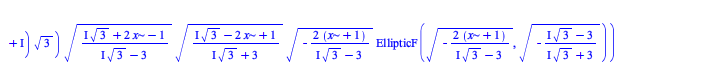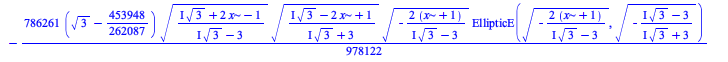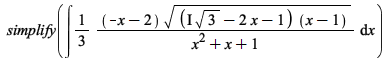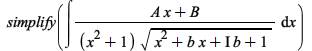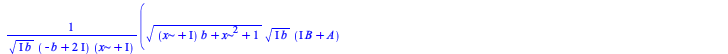| > | ![`assuming`([simplify(int(`/`(`*`(arctan(`+`(`*`(z, `*`(sqrt(2))), `-`(1)))), `*`(`+`(`*`(`^`(z, 2)), 1))), z))], [`<`(0, z)]);](advanced-math/AdvancedMath_126.gif) |
  |
| > |  |
     |
| > |  |
 |
| > |  |
       |
| > | ![`assuming`([int(BesselJ(n, x), x)], [n::odd]);](advanced-math/AdvancedMath_145.gif){kind=small} |
 |
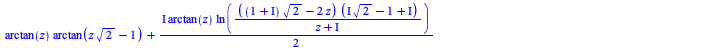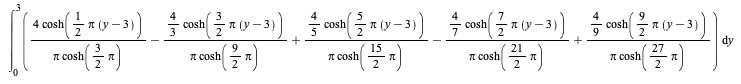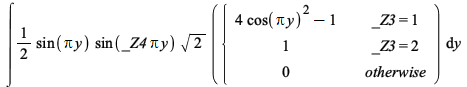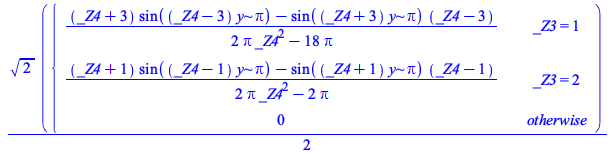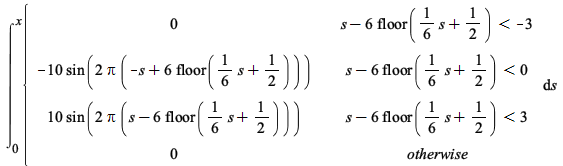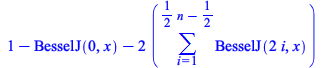Maple now performs this change of variables correctly.
| > |  |
 |
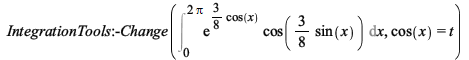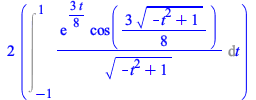The integral transforms of the inttrans package have also added more functionality - see What's New in Integral Transforms.
The definition of the JacobiP function has been extended to cases when the 2nd or 3rd argument is a negative integer.
In Maple 2019 and earlier, the following used to return 
or unevaluated:
| > |  |
 |
| > |  |
 |
| > |  |
 |
| > |  |
 |
| > |  |
 |
The Logic package contains a number of new routines for understanding the structure of logical expressions.
Incidence graph and primal graph
The new IncidenceGraph and PrimalGraph command return Graph objects which encode the incidence graph and the primal graph of a logical expression.
If e is a Boolean expression in conjunctive normal form (CNF), the primal graph of e is a graph whose vertices are the variables of e. An edge exists between two variables if these variables occur together in a clause of e, in either negated or non-negated form.
In the following example, the variables a and b share an edge because they appear together in the first clause, while a and c do not share an edge because they appear in distinct clauses.
![Typesetting:-mprintslash([PG := `Graph 1: an undirected unweighted graph with 4 vertices and 5 edge(s)`], [GRAPHLN(undirected, unweighted, [a, b, c, d], Array(%id = 18446744078203540534), `GRAPHLN/tab...](advanced-math/AdvancedMath_163.gif){kind=small} |
![GraphTheory:-DrawGraph(PG, size = [200, 200]);](advanced-math/AdvancedMath_164.gif){kind=small}
 |
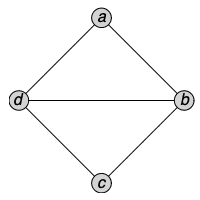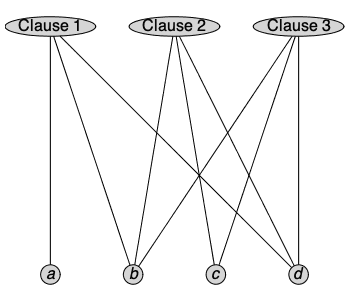
Similarly, if e is a Boolean expression in CNF, the incidence graph of e is a bipartite graph whose vertices correspond to the variables and clauses of e. Edges in the graph consist of pairs (v,c) where v is a variable and c is a clause, and clause c contains v in negated or non-negated form.
In the example seen earlier, the vertex Clause 1 shares edges with variables a, b, and d because each of these appears in the first clause of expr, but does not share an edge with c as it does not appear in this clause.
![Typesetting:-mprintslash([IG := `Graph 2: an undirected unweighted graph with 7 vertices and 9 edge(s)`], [GRAPHLN(undirected, unweighted, [a, b, c, d,](advanced-math/AdvancedMath_167.gif){kind=small} |
![GraphTheory:-DrawGraph(IG, size = [350, 300]);](advanced-math/AdvancedMath_168.gif){kind=small}
 |
Symmetry group
The new SymmetryGroup command returns a Group object describing the group of symmetries of a logical expression.
Let e be a logical expression with variables 
. A symmetry is an 
which maps each variable 
to either 
or 
for some 
, while preserving the structure of e. Symmetry detection is an important problem in the simplification of logical expressions and especially in determining satisfiability, as a straightforward effort to find solutions for a highly symmetric expression could waste resources exploring paths which are the symmetric analogues of paths already visited.
In this example, we can see that the symmetry group of this logical expression has order 2:
 |
 |
The generators of the symmetry group correspond to variables and clauses of the input expression. If we wish to see the correspondence, we can request both the group and the expressions using the output option:
![SymmetryGroup(expr, output = [expressions, group]);](advanced-math/AdvancedMath_181.gif){kind=small}
 |
Examining the above output and comparing the elements of the first list with the generators of the symmetry group, we can see that the symmetry discovered here is the one which leaves variable 
unchanged but which maps 
to 
.
NumberTheory:-JordanTotient
The new JordanTotient command in the NumberTheory package computes the 
th Jordan totient of a positive integer 
, defined as the number of 
-tuples ![a[1], () .. (), a[k];](advanced-math/AdvancedMath_189.gif){kind=small}
of positive integers such that the greatest common divisor ![gcd(a[1], () .. (), a[k], n);](advanced-math/AdvancedMath_190.gif){kind=small}
is equal to 
. This generalizes the Euler totient, which is the special case in which 
.
| > | with( NumberTheory ): |
| > | seq( Totient( n ) = JordanTotient( 1, n ), n = 1 .. 10 ); |
 |
| > | seq( JordanTotient( 2, n ), n = 1 ..10 ); |
 |
| > | Matrix( 10, 10, JordanTotient ); |
![rtable(1 .. 10, 1 .. 10, [[1, 1, 2, 2, 4, 2, 6, 4, 6, 4], [1, 3, 8, 12, 24, 24, 48, 48, 72, 72], [1, 7, 26, 56, 124, 182, 342, 448, 702, 868], [1, 15, 80, 240, 624, 1200, 2400, 3840, 6480, 9360], [1, ...](advanced-math/AdvancedMath_195.gif) |
The limit command has a new option parametric. If specified, limit will attempt to return a (piecewise) answer that is correct for all real parameter values.
| > |  |
 |
| > |  |
![Typesetting:-mprintslash([PIECEWISE([0, `<`(a, 0)], [1, a = 0], [infinity, `<`(0, a)], [Limit(`^`(x, a), x = infinity), otherwise])], [piecewise(`<`(a, 0), 0, a = 0, 1, `<`(0, a), infinity, Limit(`^`(...](advanced-math/AdvancedMath_199.gif) |
Simplification
abs, csgn, signum, and sqrt have improved normalization and simplification:
| > |  |
| > |  |
 |
| > |  |
 |
| > |  |
 |
| > |  |
 |
| > | ![`assuming`([sqrt(`*`(`^`(a, 2)))], [`<`(0, Re(a))]);](advanced-math/AdvancedMath_209.gif){kind=small} |
 |
| > | ![`assuming`([sqrt(`*`(`^`(a, 2)))], [`<`(Re(a), 0)]);](advanced-math/AdvancedMath_211.gif){kind=small} |
 |
radnormal is now more careful at simplifying expressions containing roots of negative numbers:
| > |  |
 |
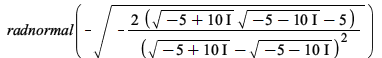simplify is more careful not to expand powers, avoiding large expressions:
| > |  |
 |
There have been some improvements in simplification of special functions:
| > |  |
 |
| > | ![`assuming`([simplify(`+`(`-`(ln(`+`(`-`(`/`(1, `*`(LambertW(z))))))), LambertW(z)), LambertW)], [Not(`<`(0, LambertW(z)))]);](advanced-math/AdvancedMath_219.gif){kind=small} |
 |
This sum can now be evaluated to a float due to an improvement in simplification of Psi of large integers:
| > |  |
 |
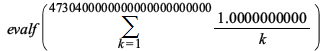Trig simplifications have been improved:
| > |  |
 |
Some improvements in simplification of piecewise functions:
| > |  |
 |
| > |  |
 |
| > |  |
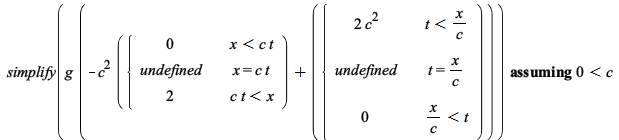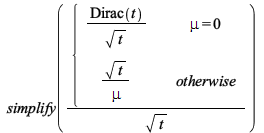![Typesetting:-mprintslash([PIECEWISE([`/`(`*`(Dirac(t)), `*`(t)), mu = 0], [`/`(1, `*`(mu)), otherwise])], [piecewise(mu = 0, `/`(`*`(Dirac(t)), `*`(t)), `/`(1, `*`(mu)))])](advanced-math/AdvancedMath_230.gif) |
simplify can now recognize that the following expressions are 0:
| > |   |
 |
| > |    |
 |
Combining expressions with trig functions is now more efficient in many cases:
| > |                                        |
   |
Miscellaneous
Some other miscellaneous improvements:
| > |  |
 |
| > |   |
 |
evalrC has been improved. The output means that abs(1/xy) can take values in the interval from 0+0*I to infinity+0*I.
| > |  |
 |
This result from isolate is now correctly expressed in terms of a RootOf:
| > |  |
 |
frontend is now more careful when recursing:
| > | ![frontend(proc (z) sign(normal(`*`(I, `*`(z)))) end proc, [`*`(I, `*`(y))]);](advanced-math/AdvancedMath_289.gif){kind=small} |
 |
