
In Maple 2020, the Group Theory package has been extended to include new tools for classifying finite groups, more searchable properties for small groups, transitive groups, perfect groups, and Frobenius groups, and new commands for computation and analysis.
| > | with( GroupTheory ): |
Classification of Finite Simple Groups
| > | c := ClassifyFiniteSimpleGroup( CyclicGroup( 19 ) ); |
| > | type( c, ':-CFSG' ); |
| > | Family( c ); |
| > | Parameters( c ); |
| > | c := ClassifyFiniteSimpleGroup( Alt( 8 ) ); |
| > | Family( c ); |
| > | Parameters( c ); |
| > | c := ClassifyFiniteSimpleGroup( PSU( 3, 3 ) ); |
| > | Family( c ); |
| > | Subfamily( c ); |
| > | ClassicalSubfamily( c ); |
| > | c := ClassifyFiniteSimpleGroup( PSp( 4, 3 ) ); |
| > | Parameters( c ); |
| > | Dimension( c ); |
| > | GroupOrder( c ); |
| > | ClassifyFiniteSimpleGroup( MathieuGroup( 10 ) ); |
| Error, (in GroupTheory:-ClassifyFiniteSimpleGroup) group is not simple |
| > | G := PerfectGroup( 1920, 1 ); |
| > | IsSimple( G ); |
| > | cs := CompositionSeries( G ); |
| > | inds := [seq]( Index( cs[ i ], cs[ i - 1 ] ), i = 2 .. numelems( cs ) ): |
| > | map( ClassifyFiniteSimpleGroup, inds ); |
| > | ClassifyFiniteSimpleGroup( 14!/2 ); |
| > | ClassifyFiniteSimpleGroup( 91091388821275796002896845335824055117112900038578882103005220458066774174756355172236381528808521951845631824767792833866989192878222394092251827671288376954168134609231184876844237947806050477334460416708128451382476800000 ); |
| > | ClassifyFiniteSimpleGroup( 2211804011555567123299716393684253115102777246104915803836223275439545886426045766402326760994180464750362624000 ); |
| > | NumSimpleGroups( 1 ); |
| > | NumSimpleGroups( 660 ); |
| > | NumSimpleGroups( 20160 ); |
| > | IsSimpleNumber( 72 ); |
| > | IsSimpleNumber( 360 ); |
| > | IsSimpleNumber( 30303030303031 ); |
| > | IsSimpleNumber( 30303030303031, 'cyclic' ); |
| > | TabulateSimpleGroups( 1 .. 1000 ); |
| > | TabulateSimpleGroups( 1 .. 10^6, 'minlierank' = 3, 'alternating' = false ); |
| > | L := map2( op, 1, TabulateSimpleGroups( 1 .. 10^15 ) ): |
| > | F := map( n -> iquo( n, 10^(length(n) - 1) ), L ): |
| > | A := evalf( [seq]( numboccur( F, i ), i = 1 .. 9 ) / nops( F ) ): |
| > | B := [seq]( log10( 1.0 + 1/i ), i = 1 .. 9 ): |
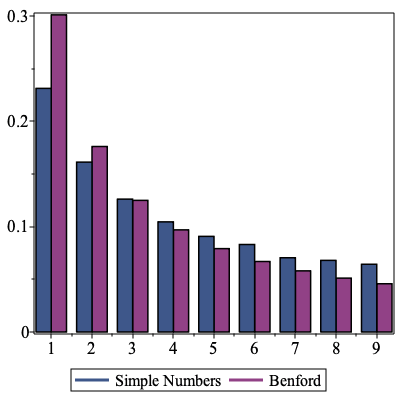
| > | use Statistics in
ColumnGraph( [ A, B ], 'legend' = [ "Simple Numbers", "Benford" ], 'offset' = 5/8 ) end use; |
 |
| > | Statistics:-ChiSquareSuitableModelTest( F,
EmpiricalDistribution( [seq](1 .. 9), 'probabilities' = B ), 'bins' = 9, 'summarize' = 'embed' ): |
Null Hypothesis: |
Sample was drawn from specified probability distribution |
||||||||||||||
Alternative Hypothesis: |
Sample was not drawn from specified probability distribution |
||||||||||||||
|
|||||||||||||||
Result: |
Rejected: This statistical test provides evidence that the null hypothesis is false. |
||||||||||||||
| > | L := [SearchSmallGroups]( 'orderclassnumber' = 2, 'elementary' = false ); |
| > | andmap( IsPGroup @ SmallGroup, L ); |
| > | L := [SearchSmallGroups]( 'orderclassnumber' = 3, 'abelian' ); |
| > | select( IsHomocyclic @ SmallGroup, L ); |
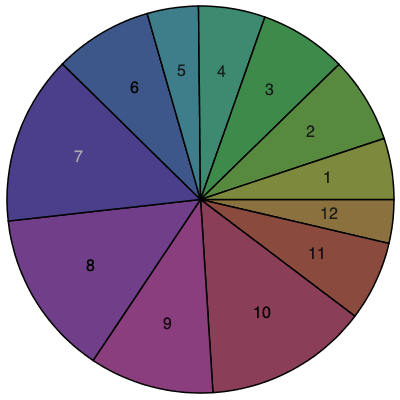
| > | L := [seq]( i = SearchPerfectGroups( 'compositionlength' = i, 'form' = "count" ), i = 1 .. 12 ); |
| > | Statistics:-PieChart( L ); |
 |
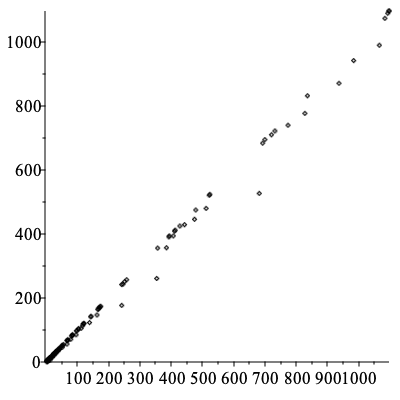
| > | A := Array([]): |
| > | i := 0: do t := SearchPerfectGroups( 'maxelementorder' > ++i, form = "count" ); A ,= t; until t = 0: |
| > | numelems( A ); |
| > | plots:-pointplot( A ); |
 |
| > | SearchPerfectGroups( 'frobenius' ); |
| > | G := PerfectGroup( 14520, 1 ): |
| > | IdentifyFrobeniusGroup( G ); |
| > | SearchFrobeniusGroups( 'primitive', 'form' = "count" ); |
| > | SearchFrobeniusGroups( 'primitive', 'abeliancomplement' = false, 'form' = "count" ); |
| > | L := [SearchFrobeniusGroups]( 'transitivity' > 1 ): |
| > | map( Transitivity @ FrobeniusGroup, L ); |
| > | IsHomocyclic( CyclicGroup( 12 ) ); |
| > | IsHomocyclic( Group( [ Perm( [[1,2]]), Perm([[3,4]]) ] ) ); |
| > | IsHomocyclic( SmallGroup( 144, 2 ) ); |
| > | IsHomocyclic( SmallGroup( 144, 3 ) ); |
| > | PermGroupRank( Alt( 5 ) ); |
| > | G := DihedralGroup( 5 ): |
| > | PermGroupRank( G ); |
| > | S := Stabilizer( 1, G ): |
| > | nops( Orbits( S ) ); |
| > | Spor := [ MathieuGroup(11), MathieuGroup(12),
MathieuGroup(22), MathieuGroup(23), MathieuGroup(24), JankoGroup( 1 ), JankoGroup( 2 ), JankoGroup( 3 ), JankoGroup( 4 ), ConwayGroup( 1 ), ConwayGroup( 2 ), ConwayGroup( 3 ), FischerGroup( 22 ), FischerGroup( 23 ), FischerGroup( 24 ), HigmanSimsGroup(), McLaughlinGroup(), HeldGroup(), RudvalisGroup(), SuzukiGroup(), ONanGroup(), HaradaNortonGroup(), LyonsGroup(), ThompsonGroup(), BabyMonster(), Monster(), TitsGroup() ]: |
| > | SporNames := map(print_preprocess,Spor): |
| > | GK := map( GruenbergKegelGraph, Spor ): |
| > | use GraphTheory in
for G in GK do HighlightVertex( G, SelfLoops( G ), 'stylesheet' = [ 'shape' = "pentagon", 'color' = "red" ] ); HighlightVertex( G, map( op, select( c -> nops(c)=1, ConnectedComponents( G ) ) ), 'stylesheet' = [ 'shape' = "7gon", 'color' = "green" ] ) end do end use: |
| > | GK := [seq]( GraphTheory:-DrawGraph( GK[ i ], 'title' = SporNames[ i ] ), i = 1 .. nops( Spor ) ): |
| > | GK := Matrix( 9, 3, GK ): |
| > | plots:-display( GK ); |
|
| > | OrderClassNumber( Symm( 5 ) ); |
| > | MaximumElementOrder( Alt( 4 ) ); |
| > | ElementOrderSum( Alt( 4 ) ); |
| > | G := Suzuki2B2( 2 ); |
| > | IsSimple( G ); |
| > | IsFrobeniusGroup( G ); |
| > | IdentifyFrobeniusGroup( G ); |
| > | IsSimple( Suzuki2B2( 128 ) ); |
| > | p := Perm( [[1,2,3],[4,6]] ); |
| > | PermShift( p, 3 ); |
| > | PermRestrict( p, {1,2,3} ); |
| > | Perm( [[1,2,3]] ) in Alt( 4 ); |
| > | PermAltSplit( Perm( [[1,2,3]] ) ); |
| > | numelems( ConjugacyClass( Perm( [[1,2,3]] ), Symm( 4 ) ) ); |
| > | numelems( ConjugacyClass( Perm( [[1,2,3]] ), Alt( 4 ) ) ); |
| > | Perm( [[1,2],[3,4]] ) in Alt( 4 ); |
| > | PermAltSplit( Perm( [[1,2],[3,4]] ) ); |
| > | numelems( ConjugacyClass( Perm( [[1,2],[3,4]] ), Symm( 4 ) ) ); |
| > | numelems( ConjugacyClass( Perm( [[1,2],[3,4]] ), Alt( 4 ) ) ); |
| > | G := FrobeniusGroup( [ 4032, 2 ] ): |
| > | IsElementary( FrobeniusKernel( G ) ); |
| > | PGroupPrime( FrobeniusKernel( G ) ); |
| > | PerfectGroup( [ 60, 1 ], 'form' = "fpgroup" ); |