
Integral transforms are special integrals that appear frequently in mathematical physics and that have remarkable properties. For Maple 2020, the implementation of these integrals has been extended in several ways, making them more useful for a variety of applications, including computing integrals, finding exact solutions to PDEs with boundary conditions (see What's New in ODEs and PDEs). Improvements include the option to compute derivatives, numeric support, an alternate definition of the Hankel transform, and the ability to compute more transforms.
As background, these integrals are represented by the commands of the inttrans package:
| > |
| (1) |
Three of these commands, addtable, savetable, and setup (new as of Maple 2020) are "administrative" commands, while the others are computational representations for definite integrals. For example,
| > |
 |
(2) |
| > |
| (3) |
For all integral transform commands, the first argument is the integrand, the second one is the dummy integration variable of a definite integral and the third one is the evaluation point (also called transform variable).
Compute derivatives: yes or no.
Generally speaking, in computer algebra, "given a function ![]() , the input
, the input ![]() should return the derivative of
should return the derivative of ![]() ". For the purpose of using integral transforms to solve differential equations, however, the implementation in previous Maple releases worked in the opposite direction: if you were to input the result of the derivative, you would receive the derivative representation. For example, to the input
". For the purpose of using integral transforms to solve differential equations, however, the implementation in previous Maple releases worked in the opposite direction: if you were to input the result of the derivative, you would receive the derivative representation. For example, to the input ![]() you would receive
you would receive ![]() . To extend the capabilities of the system and have the best result in any scenario, a new command, setup, has been added to the package, so that you can set whether or not to compute derivatives, and the default has been changed to computederivatives = true while the previous behavior is obtained only if you input
. To extend the capabilities of the system and have the best result in any scenario, a new command, setup, has been added to the package, so that you can set whether or not to compute derivatives, and the default has been changed to computederivatives = true while the previous behavior is obtained only if you input ![]() . To query about the status of this new setting enter
. To query about the status of this new setting enter
| > |
| (1.1) |
and so differentiating returns the derivative computed
| > |
| (1.2) |
while changing this setting to work as in previous releases you have this computation reversed: you input the output ![]() and you get the corresponding input
and you get the corresponding input
| > |
| (1.3) |
| > |
| (1.4) |
Reset the value of computederivatives
| > |
| (1.5) |
| > |
| (1.6) |
In summary: by default, derivatives of all the 11 integral transforms are now computed. This setting can be changed any time you want within a Maple session without restarting, and changing it does not have any impact on the performance of intsolve, dsolve and pdsolve to solve differential equations using integral transforms.
Numerical evaluation
In previous releases, integral transforms had no numerical evaluation implemented. This is in the process of changing. So, for example, to numerically evaluate the inverse laplace transform (invlaplace command), three different algorithms have been implemented: Gaver-Stehfest, Talbot and Euler, following the presentation by Abate and Whitt, "Unified Framework for Numerically Inverting Laplace Transforms", INFORMS Journal on Computing 18(4), pp. 408-421, 2006.
For example, consider the exact solution to this partial differential equation subject to initial and boundary conditions
| > |
| > |
Note that these two conditions are not entirely compatible: the solution returned cannot be valid for ![]() and
and ![]() simultaneously. However, a solution discarding that point does exist and is given by
simultaneously. However, a solution discarding that point does exist and is given by
| > |
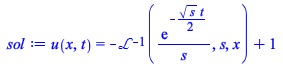 |
(2.1) |
Verifying the solution, one condition remains to be tested
| > |
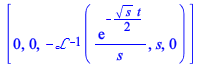 |
(2.2) |
Since we now have numerical evaluation rules, we can test that what looks different from 0 in the above is actually 0.
| > |
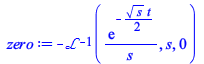 |
(2.3) |
Add a small number to the initial value of t to skip the point ![]()
| > |
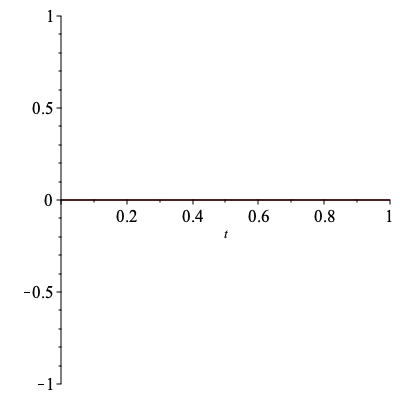 |
The default method used is the method of Euler sums and the numerical evaluation is performed as usual using the evalf command. For example, consider
| > |
| (2.4) |
The Laplace transform of F is given by
| > |
![Typesetting:-mprintslash([LT := `+`(`/`(`*`(`/`(1, 2), `*`(`^`(2, `/`(1, 2)), `*`(`^`(Pi, `/`(1, 2)), `*`(exp(`+`(`-`(`/`(`*`(`/`(1, 2)), `*`(s))))))))), `*`(`^`(s, `/`(3, 2)))))], [`+`(`/`(`*`(`/`(1,...](integral-transforms/Integral Transforms_42.gif) |
(2.5) |
and the inverse Laplace transform of LT in inert form is
| > |
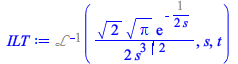 |
(2.6) |
Since by construction ![]() , at
, at ![]() we have
we have
| > |
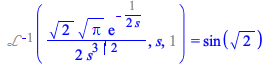 |
(2.7) |
This inert form on the left-hand side is numerically evaluated next, directly, without symbolically resolving it to be equal to ![]() . The result of both sides is consistent:
. The result of both sides is consistent:
| > |
| (2.8) |
In addition to the standard use of evalf to numerically evaluate inverse Laplace transforms, one can invoke each of the three different methods implemented using the MathematicalFunctions:-Evalf command
| > |
| (2.9) |
| > |
| (2.10) |
| > |
| (2.11) |
| > |
| (2.12) |
Regarding the method we use by default: from a numerical experiment with varied problems, we have concluded that our implementation of the Euler (sums) method is faster and more accurate than the other two.
Two Hankel transform definitions
In previous Maple releases, the definition of the Hankel transform was given by
![]()
where ![]() is the
is the ![]() function. This definition, sometimes called alternative definition of the Hankel transform, has the advantage of having a large table of transforms presented in the literature (ref.[1]) but has the inconvenience of the square root
function. This definition, sometimes called alternative definition of the Hankel transform, has the advantage of having a large table of transforms presented in the literature (ref.[1]) but has the inconvenience of the square root ![]() in the integrand, complicating the form of the Hankel transform for the Laplacian in cylindrical coordinates. On the other hand, the other definition in the literature,
in the integrand, complicating the form of the Hankel transform for the Laplacian in cylindrical coordinates. On the other hand, the other definition in the literature,
![]()
has the advantage that, with it, the Hankel transform of  is given by the simple ODE form
is given by the simple ODE form ![]() . Several other transforms also acquire a simpler form. So for Maple 2020 we added an algorithm that takes formulas for one definition and transforms them into formulas for the other definition, and have aligned Maple with this simpler definition (no
. Several other transforms also acquire a simpler form. So for Maple 2020 we added an algorithm that takes formulas for one definition and transforms them into formulas for the other definition, and have aligned Maple with this simpler definition (no ![]() in the integrand), while keeping the previous definition as an alternative.
in the integrand), while keeping the previous definition as an alternative.
Hence, by default, when you load the inttrans package, the new definition in use for the Hankel transform is
| > |
| (3.1) |
You can change this default so that Maple works with the alternative definition as in previous releases. For that purpose, use the new inttrans:-setup command (which you can also use to query about the definition in use at any moment):
| > |
| (3.2) |
The change in the default definition implemented in Maple 2020 is automatically taken into account by other parts of the Maple library using the Hankel transform. For example, the differentiation rule with the new definition is
| > |
| (3.3) |
This differentiation rule resembles (is connected to) the differentiation rule for BesselJ, and this is another advantage of the new definition.
| > |
 |
(3.4) |
Furthermore, several transforms have acquired a simpler form, as for example:
| > |
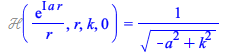 |
(3.5) |
Let's compare: make the definition be as in previous releases.
| > |
| (3.6) |
| > |
| (3.7) |
The differentiation rule with the previous (alternative) definition was not as simple:
| > |
| (3.8) |
And the transform ![]() was also not so simple:
was also not so simple:
| > |
 |
(3.9) |
Reset to the new default value of the definition.
| > |
| (3.10) |
| > |
| (3.11) |
More integral transform results
Maple is now able to compute more transforms. For example, for the Hankel transform, consider the operators
| > | 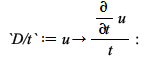 |
Being able to transform these operators into algebraic expressions or differential equations of lower order is key for solving ODE and PDE problems with Boundary Conditions. To illustrate that, set ![]() , a more convenient setting to use transforms to simplify differential equations, and insert some values in formula_minus
, a more convenient setting to use transforms to simplify differential equations, and insert some values in formula_minus
| > |
| (4.1) |
| > |
 |
(4.2) |
Its Hankel transform is
| > |
| (4.3) |
An example with formula_plus:
| > |
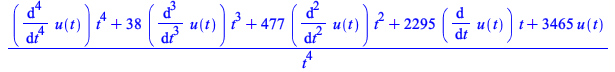 |
(4.4) |
| > |
| (4.5) |
Not just differential operators but also several new transforms are now computable
| > |
![Typesetting:-mprintslash([PIECEWISE([`/`(`*`(Dirac(k)), `*`(k)), nu = 0], [`/`(`*`(nu), `*`(`^`(k, 2))), otherwise])], [piecewise(nu = 0, `/`(`*`(Dirac(k)), `*`(k)), `/`(`*`(nu), `*`(`^`(k, 2))))])](integral-transforms/Integral Transforms_106.gif) |
(4.6) |
| > |
![Typesetting:-mprintslash([PIECEWISE([`/`(`*`(Dirac(k)), `*`(k)), And(nu = 0, m = 0)], [`/`(`*`(`^`(2, `+`(m, 1)), `*`(`^`(k, `+`(`-`(m), `-`(2))), `*`(GAMMA(`+`(1, `*`(`/`(1, 2), `*`(m)), `*`(`/`(1, 2...](integral-transforms/Integral Transforms_108.gif) |
(4.7) |
| > |
| (4.8) |
| > |
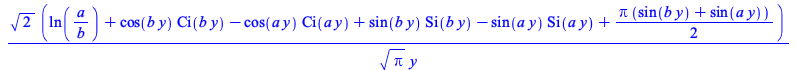 |
(4.9) |
| > | ![`assuming`([fouriersin(`/`(`*`(ln(abs(`/`(`*`(`+`(a, x)), `*`(`+`(x, `-`(a))))))), `*`(`^`(x, 2))), x, y)], [`<`(0, a)]);](integral-transforms/Integral Transforms_113.gif) |
| (4.10) |
| > | ![`assuming`([fouriersin(`/`(`*`(ln(abs(`/`(`*`(`+`(`*`(`^`(a, 2)), `*`(`^`(x, 2)))), `*`(`+`(`-`(`*`(`^`(b, 2))), `*`(`^`(x, 2)))))))), `*`(x)), x, y)], [`<`(0, a), `<`(0, b)]);](integral-transforms/Integral Transforms_115.gif) |
| (4.11) |
| > | ![`assuming`([fouriercos(`/`(`*`(ln(abs(`/`(`*`(`+`(a, x)), `*`(`+`(x, `-`(a))))))), `*`(x)), x, y)], [`<`(0, a)]);](integral-transforms/Integral Transforms_117.gif) |
| (4.12) |